Towards Efficient Coordination in Multi-Agent Reinforcement Learning through Hybrid Information-Driven Approaches

Abstract

This paper introduces a novel framework to enhance coordination in multi-agent reinforcement learning (MARL) systems by integrating mutual information (MMI) principles with information-driven strategies. Firstly, we propose a variational approach leveraging MMI to promote coordinated behaviors among agents by regulating the cumulative return alongside the simultaneous mutual information between multi-agent actions. Through the introduction of a latent variable inducing nonzero mutual information and the application of a variational bound, a tractable lower bound is derived for the MMI-regularized objective function. This bound combines maximum entropy reinforcement learning with reducing uncertainty in other agents\' actions. Subsequently, we present a practical algorithm, Variational Maximum Mutual Information Multi-Agent Actor-Critic (VM3-AC), utilizing policy iteration to maximize the derived lower bound, following a centralized learning with decentralized execution (CTDE) paradigm. Secondly, we explore the challenges of large state spaces and limited computational resources in distributed multi-agent systems, proposing a hybrid information-driven MARL approach. This approach integrates information-theoretic models as heuristics to aid navigation in sparse state spaces, complemented by information-based rewards within an RL framework to learn higher-level policies efficiently. Our preliminary findings suggest that this hybrid approach could enhance exploration efficiency significantly, demonstrating approximately three orders of magnitude improvement over naive baseline metrics. Although still in its early stages, this work presents a promising direction for future research in achieving efficient coordination in MARL systems.

Introduction

I. INTRODUCTION

In recent years, Multi-Agent Reinforcement Learning (MARL) has emerged as a powerful paradigm for enabling intelligent decision-making in complex, decentralized systems comprising multiple interacting agents. The ability of these agents to learn and adapt their behaviors based on interactions with their environment holds promise for applications ranging from autonomous vehicles and robotic swarms to collaborative multi-agent games and resource allocation in distributed networks. However, coordinating the actions of multiple agents in such environments poses a significant challenge. Traditional approaches often rely on centralized control or handcrafted coordination mechanisms, which can be impractical or even infeasible in real-world scenarios due to issues such as communication constraints, scalability, and the need for adaptability to dynamic environments.

To address these challenges, researchers have turned to principles from information theory to develop novel coordination strategies in MARL systems. One such principle is mutual information (MMI), which quantifies the statistical dependence between random variables and has found applications in various fields, including communication, signal processing, and machine learning. In this paper, we propose a new framework that leverages MMI to facilitate efficient coordination among agents in MARL systems. Our approach is based on a variational method that introduces a latent variable to induce nonzero mutual information between the actions of multiple agents. By regularizing the cumulative return with simultaneous mutual information, our framework encourages agents to learn coordinated behaviors while maximizing their rewards.

Furthermore, to address the challenges posed by large state spaces and limited computational resources in distributed multi-agent systems, we propose a hybrid approach that combines information-theoretic models with reinforcement learning (RL) techniques. This approach utilizes information-driven heuristics to aid navigation in sparse state spaces, complemented by information-based rewards within an RL framework to learn higher-level policies efficiently. The contributions of this paper are twofold: Firstly, we present a variational approach to mutual information-based coordination in MARL, which provides a tractable and interpretable framework for encouraging coordinated behaviors among agents. Secondly, we introduce a hybrid information-driven MARL approach that addresses the challenges of exploration efficiency in sparse state spaces while leveraging the benefits of mutual information for coordination. In the following sections, we provide a detailed description of our proposed framework, including the mathematical formulation, algorithmic details, and experimental results demonstrating the effectiveness of our approach in various coordination tasks. Additionally, we discuss related work in the field and outline avenues for future research. Overall, we believe that our contributions will advance the state-of-the-art in MARL and pave the way for more efficient and scalable coordination strategies in complex multi-agent systems.

As technology evolves, sensors become more sophisticated while simultaneously becoming smaller and more affordable. This progress enables the development of intricate sensor applications powered by machine learning and artificial intelligence algorithms. One notable trend is the integration of diverse autonomous sensors into sophisticated sensor networks. These networks can be managed either centrally or decentrally, offering flexibility in their control. However, despite these advancements, several challenges persist in effectively designing and managing such networks. One prominent issue is the complexity of algorithms, which escalates as the number of agents or sensors in the network grows. This challenge poses hurdles in the scalability and efficient management of large-scale sensor networks [1,2].

With the success of RL in the single-agent domain [3, 4] MARL is being actively studied and applied to real-world problems such as traffic control systems and connected self-driving cars, which can be modeled as multi-agent systems requiring coordinated control [5, 6].

A common approach to tackle this challenge is employing a fully centralized critic within the framework of centralized training with decentralized execution (CTDE) [7,8,9,10]. For instance, methods like MADDPG [11] utilize a centralized critic to train individual decentralized policies for each agent, while approaches like COMA employ a shared centralized critic to train all decentralized policies collectively [12]. However, these methods assume that decentralized policies operate independently, treating the joint policy as a simple product of each agent's policy. This assumption limits the agents' ability to learn coordinated behaviors since it overlooks the influence of other agents [13,14]. Recently, researchers have explored the use of mutual information (MI) between actions of multiple agents as an intrinsic reward to foster coordination in Multi-Agent Reinforcement Learning (MARL) [15]. In such frameworks, MI serves as a measure of social influence, aiming to maximize the combined rewards and social influence among agents' actions. While effective for sequential social dilemma games, these approaches require causality between actions and may not straightforwardly address the coordination of simultaneous actions in certain multi-agent scenarios where cooperation towards a common goal is essential.

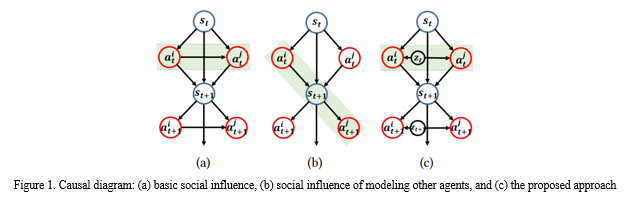
Figure 1 presents a series of causal diagrams illustrating different concepts related to social influence in multi-agent systems:

a. Basic Social Influence: This diagram depicts the basic concept of social influence, where each agent's action influences the subsequent actions of other agents in the system. The arrows represent causal relationships, indicating the direction of influence between agents. In this scenario, agents influence each other's actions directly, leading to a network of interdependencies.

b. Social Influence of Modelling Other Agents: In this diagram, the concept of social influence is extended to include the modeling of other agents' behaviors. Each agent not only influences the actions of others but also considers the expected behaviors of other agents when making decisions. This modeling of other agents' behaviors introduces a higher level of complexity to the social influence dynamics, as agents must anticipate and respond to the anticipated actions of their peers.

c. The Proposed Approach: This diagram presents the proposed approach, which integrates mutual information (MI) between actions of multiple agents as a measure of social influence. Unlike the previous diagrams, which focus on direct causal relationships between agents' actions, the proposed approach considers the information flow between agents. By maximizing MI between actions, agents aim to coordinate their behaviors effectively while taking into account the influence of other agents in the system. This approach offers a more nuanced understanding of social influence dynamics, facilitating coordinated decision-making among multiple agents in complex environments. Overall, these causal diagrams provide visual representations of different aspects of social influence in multi-agent systems, highlighting the evolution of concepts from basic influence dynamics to the proposed approach leveraging mutual information for enhanced coordination.

II. RELATED WORK

Multi-agent reinforcement Learning (MARL) has garnered significant attention in recent years due to its potential applications in various domains, including robotics, autonomous systems, and distributed optimization. In this section, we review relevant literature focusing on coordination strategies in MARL, information-theoretic approaches, and hybrid frameworks combining reinforcement learning with information-driven techniques. Traditional approaches to coordinating multiple agents in MARL systems often rely on centralized control or handcrafted coordination mechanisms. However, these methods may suffer from scalability issues, communication overhead, and lack of adaptability to dynamic environments.

Mutual information (MI) serves as a vital metric in understanding the relationship between two variables, and its utility extends to Multi-Agent Reinforcement Learning (MARL) as well [16]. Recent studies have highlighted MI as an effective intrinsic reward for MARL tasks, showcasing its potential to enhance agent performance [17]. For instance, researchers have explored MI-based intrinsic rewards for empowerment, aiming to maximize the MI between an agent's actions and its subsequent states. Additionally, intrinsic rewards have been devised to capture the influence of an agent's decisions, leveraging MI between an agent's actions or states and those of other agents [18]. Notably, some works have focused on fostering coordination among agents by emphasizing the social influence of intrinsic reward, which measures the MI between the actions of multiple agents. These approaches have demonstrated promising results, particularly in sequential social dilemma scenarios [15]. While previous works have delved into correlated policies through various methodologies, such as explicit modeling and recursive reasoning frameworks, our approach diverges by prioritizing the maximization of MI between actions of multiple agents. This emphasis on MI serves as a comprehensive measure of correlation, aiming to foster effective coordination among agents in MARL settings [19,20].

A promising direction is to leverage principles from information theory to design coordination strategies. The concept of mutual information (MI) has been particularly influential in this regard. In their work, [21] proposed using MI as a measure of interaction between agents, enabling them to learn communication protocols in cooperative tasks. Furthermore, [22] introduced a framework based on MI gradients for learning communication protocols in partially observable environments, demonstrating improved coordination among agents. Information theory provides a rich theoretical framework for understanding and quantifying the flow of information in complex systems. In the context of MARL, mutual information has been utilized to measure the statistical dependence between actions of multiple agents, thereby facilitating coordination.

The work of [23] introduced a variational approach to mutual information-based coordination in MARL, wherein agents learn to maximize mutual information between their actions while optimizing their rewards. This approach provides a tractable framework for encouraging coordinated behaviors among agents. Hybrid approaches that combine reinforcement learning with information-driven techniques offer a promising avenue for addressing challenges such as exploration efficiency and scalability in MARL systems. In their study, [24] proposed a hybrid approach that integrates information-theoretic models as heuristics to aid navigation in sparse state spaces. By coupling information-based rewards with reinforcement learning frameworks, the authors demonstrated significant improvements in exploration efficiency compared to baseline methods. In summary, coordination strategies in MARL play a crucial role in enabling agents to achieve complex goals in dynamic and uncertain environments. Information-theoretic approaches, particularly those based on mutual information, offer a principled framework for facilitating coordination among agents. Furthermore, hybrid frameworks that combine reinforcement learning with information-driven techniques hold promise for addressing challenges such as exploration efficiency and scalability in MARL systems.

III. RESEARCH METHODOLOGY

The research methodology proposed for this study encompasses a systematic approach to address the objective of enhancing coordination among multiple agents in decentralized environments using mutual information-based strategies. Beginning with a clear problem formulation, the methodology proceeds with an extensive literature review to identify existing gaps and limitations in current methodologies. Subsequently, a mathematical framework is developed, laying the foundation for a variational approach to derive a tractable lower bound on the mutual information regularized objective function. This formulation is then translated into a practical algorithm, namely the Variational Maximum Mutual Information Multi-Agent Actor-Critic (VM3-AC), which integrates policy iteration within centralized learning with decentralized execution (CTDE) paradigm. Furthermore, the methodology proposes the integration of information-theoretic models as heuristics to aid navigation in sparse state spaces, forming a hybrid framework that combines information-based rewards with reinforcement learning techniques. Experimental setups are carefully designed to evaluate the proposed methodology across various benchmark tasks, assessing coordination efficiency, exploration efficiency, scalability, and adaptability to dynamic environments. Implementation details ensure reproducibility and transparency, while results analysis involves quantitative evaluation and statistical validation to interpret the performance metrics and derive meaningful insights. The discussion and conclusion sections summarize key findings, discuss implications, and outline future research directions, thereby contributing to advancing the state-of-the-art in decentralized multi-agent decision-making.

In Figure 2, the red box depicts the overall operation of the proposed Variational Maximum Mutual Information Multi-Agent Actor-Critic (VM3-AC) framework after training. After the training phase, which involves learning coordinated behaviors among multiple agents through maximizing mutual information (MI) between their actions, the trained agents are deployed for execution in their respective environments. During execution, each agent operates in a decentralized manner, making decisions based on its local observations and learned policies. However, despite the decentralized execution, the agents maintain communication with each other to exchange relevant information as needed. This communication ensures that the agents remain coordinated and aligned toward achieving the common goal, even in dynamic and uncertain environments. Furthermore, the VM3-AC framework allows for adaptability to changes in the environment or task requirements, enabling the agents to continuously refine their behaviors and strategies over time. Overall, the operation within the red box highlights the robustness and effectiveness of the VM3-AC framework in facilitating coordinated decision-making among multiple agents in real-world scenarios.

MI between agents’ actions has been considered as an intrinsic reward to promote coordination in MARL [15]. Under this framework, one basically aims to find the policy that maximizes the weighted sum of the return and the MI between multi-agent actions. Thus, the MI-regularized objective function for joint policy ???? is given by:

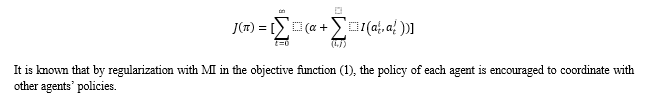
A. Centralized Training Phase

1. Initialization: Initialize the parameters for each agent, including actor parameters ????????, critic parameters ????????, entropy coefficient parameters ????????, and state normalization parameters ????????.
2. Episodic Training Loop: Iterate over episodes.
3. Initialization within Each Episode: Set the initial state ????0 and allow each agent to observe its initial observation ????????0.
4. Time Step Loop within Each Episode: Iterate over time steps ???? until the terminal state is reached. Generate a random noise vector ???????? from a normal distribution. Select actions for each agent based on their observation and the generated noise vector using their respective policies ????????. Execute the selected actions and observe the next state and reward for each agent. Store the transitions in the replay buffer ???? for later training.
5. Gradient Step Loop within Each Episode: Iterate over gradient steps for updating the network parameters. Sample a minibatch from the replay buffer ???? and generate noise vectors ???????? for each transition. Update the actor and critic network parameters ???????? and ???????? by minimizing the defined loss functions. Update the parameters ???????? and ???????? for state normalization.
6. Update Critic Target Parameters: Update the target critic network parameters ???????? using the moving average method to stabilize training.

B. Decentralized Execution Phase

1. Initialization: Set the initial state ????0 and allow each agent to observe its initial observation ????????0.
2. Environment Step Loop: Iterate over environment steps. Select actions for each agent based on their observation using their policies ????????. Execute the selected actions and observe the next state for each agent.

In summary, the algorithm consists of two main phases: the centralized training phase, where agents learn to coordinate their actions through centralized training, and the decentralized execution phase, where trained agents interact with the environment autonomously based on their learned policies. During training, agents update their parameters using gradient descent to improve their policies and value functions. During execution, agents act independently based on their observations and learned policies, facilitating decentralized decision-making in real-world scenarios.

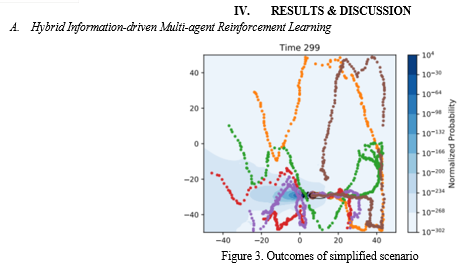
Figure 1 showcases the outcomes of a simplified scenario involving five agents tasked with localizing a plume, utilizing an information-based motion heuristic exclusively. The top panel provides a visual representation of the two-dimensional plume environment, with small circles indicating the history of measurement locations by each agent, distinguished by their respective IDs. The shaded background illustrates the normalized posterior probability distribution of the plume's source location, as estimated collectively by the agents at time step 299.

Notably, the distribution is concentrated around the true plume source location denoted by the black X. In the second panel, a history of concentration measurements made by the agents is depicted, mostly scattered around zero with variance attributed to user-defined noise, indicated by dashed black lines representing 1σ. The bottom two panels present the history of information gain (measured by DKL) for the simulation, represented by a thick blue line. For comparison, the histories of two separate simulations using only cost weight as a motion heuristic (orange) and entirely random motion (green) are shown. The fluctuations observed are a consequence of noisy measurements. Notably, the information-based motion heuristic proves to be over three orders of magnitude more efficient compared to the baseline random methods in the long run.

As we introduce complexities into the problem, such as removing communication abilities among agents, inferring their states, and imposing costs on measurements, the optimization task becomes considerably more challenging. Particularly, incorporating these factors into the optimization problem escalates the computational costs, rendering a fully information theory-based sensor optimization approach impractical. While Reinforcement Learning (RL) offers potential for learning effective policies in such scenarios, the computational expense of training RL models for fully estimating partially observable state spaces with a noninformative prior is prohibitive. Consequently, we propose an alternative strategy that combines RL with heuristic models, utilizing RL for high-level decision-making and leveraging information-based heuristics for determining agent motion. This approach aims to strike a balance between computational efficiency and decision-making efficacy, allowing agents to make informed decisions while navigating complex environments efficiently.

The reward structure is driven by the internal assumptions of the agent, utilizing the distance between the actual source location and the agent's current best estimate of the source location, along with the achieved information gain. Additionally, part of the reward is based on logical assumptions regarding favorable behavior, such as reducing energy consumption and maintaining a low profile to avoid detection. Initially, at the start of training, the information-based component predominates. However, as estimation accuracy improves and information gain increases, the additional action-based reward gains prominence. The goal is to facilitate the learning of desired behaviors under logical assumptions, without overly guiding the agent's actions. For instance, when an agent has high confidence in its source location estimate, it's preferable to conserve resources and minimize movement or communication to avoid detection.

This approach enables agents to adapt their behaviors intelligently based on available information and strategic considerations, promoting efficient operation in dynamic environments.

In comparing mutual information with entropy, the proposed mutual information (MI) framework focuses on maximizing the sum of action entropy and the negative cross-entropy of the variational conditional distribution concerning the true conditional distribution. This approach establishes a lower bound on the mutual information between actions. As mentioned earlier, optimizing this sum enhances both exploration and predictability regarding other agents' actions. Consequently, the MI framework facilitates correlated exploration among agents, promoting coordinated behaviors and effective decision-making in multi-agent systems.

Conclusion

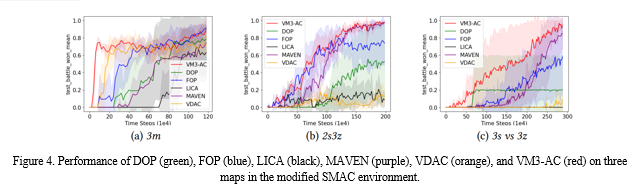
In conclusion, this research has introduced a novel Mutual Information (MI) framework for Multi-Agent Reinforcement Learning (MARL), aiming to enhance coordination and decision-making among multiple agents in complex environments. By maximizing the sum of action entropy and the negative cross-entropy of the variational conditional distribution relative to the true conditional distribution, the proposed MI framework establishes a lower bound on the mutual information between agent actions. This approach not only fosters exploration and predictability of other agents\' actions but also promotes correlated exploration among agents, leading to more effective coordination in achieving common goals. Furthermore, the integration of logical assumptions into the reward structure incentivizes behaviors aligned with operational efficiency and low-profile operation, contributing to adaptive and intelligent decision-making. Overall, the proposed MI framework offers a promising avenue for addressing challenges in MARL, paving the way for enhanced coordination and cooperation in multi-agent systems. Furthermore, a novel approach to mutual information (MI)-based coordinated MARL is proposed, aiming to induce coordination among agents\' concurrent actions under the centralized training with decentralized execution (CTDE) paradigm. The approach involves injecting a common correlation-inducing random variable into each policy network and expressing the MI between actions induced by this variable in a tractable form using a variational distribution. The resulting objective function combines maximum entropy RL with predictability enhancement (or uncertainty reduction) for other agents\' actions, fostering correlated exploration. Evaluation of the derived algorithm, VM3-AC, on both continuous and discrete action tasks, has demonstrated its superiority over state-of-the-art baselines, particularly in tasks requiring high-quality coordination among agents. In this position paper, the concept of hybrid information-driven multi-agent reinforcement learning (MARL) is introduced, emphasizing the power of leveraging information metrics for state space estimation while utilizing reinforcement learning (RL) to learn decision-making policies. The experiments focus on agent cooperation facilitated solely through communication triggered by specific actions. Moving forward, the exploration of alternative agent training methods such as Multi-Agent Deep Deterministic Policy Gradient (MADDPG), Reinforced Inter-Agent Learning (RIAL), and Differentiable Inter-Agent Learning (DIAL) is planned. Additionally, the integration of decentralized Markov Chain Monte Carlo (MCMC) methods for full posterior inference in non-discretized, non-conjugate models is underway to enhance the information aspect of the framework. Scalability is another focus, with ongoing efforts to develop high-fidelity, discrete-event simulations for modeling wireless communication protocols and accommodating a larger number of agents. However, one limitation of the approach is the necessity for communication between agents when sharing a common variable. To address this, alternative methods, including sharing a Gaussian random sequence generator and injecting the mean vector into the latent vector during execution, are introduced. Although these methods require reference timing information and entail some communication overhead, the ablation study has shown promising results. Additionally, communication is recognized as a promising avenue for enhancing coordination between agents, with plans to explore its integration with the mutual information framework in future research endeavors. Overall, the work lays the groundwork for advancing hybrid information-driven MARL approaches and addressing challenges in multi-agent coordination and decision-making.

References

[1] J. Chen, S. Chen, Q. Wang, B. Cao, G. Feng, and J. Hu. 2019. iRAF: A deep reinforcement learning approach for collaborative mobile edge computing IoT networks. IEEE Internet of Things Journal 6(4): 7011–7024. [2] X. Wang, C. Wang, X. Li, V. C. Leung, and T. Taleb. 2020. Federated deep reinforcement learning for internet of things with decentralized cooperative edge caching. IEEE Internet of Things Journal. [3] Timothy P Lillicrap, Jonathan J Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuval Tassa, David Silver, and Daan Wierstra. 2015. Continuous control with deep reinforcement learning. arXiv preprint arXiv:1509.02971 (2015) [4] Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Andrei A Rusu, Joel Veness, Marc G Bellemare, Alex Graves, Martin Riedmiller, Andreas K Fidjeland, Georg Ostrovski, et al. 2015. Human-level control through deep reinforcement learning. Nature 518, 7540 (2015), 529–533. [5] CP Andriotis and KG Papakonstantinou. 2019. Managing engineering systems with large state and action spaces through deep reinforcement learning. Reliability Engineering & System Safety 191 (2019), 106483. [6] Minne Li, Zhiwei Qin, Yan Jiao, Yaodong Yang, Jun Wang, Chenxi Wang, Guobin Wu, and Jieping Ye. 2019. Efficient ridesharing order dispatching with mean field multi-agent reinforcement learning. In The World Wide Web Conference. 983–994. [7] Shariq Iqbal and Fei Sha. 2018. Actor-attention-critic for multi-agent reinforcement learning. arXiv preprint arXiv:1810.02912 (20 [8] Jeewon Jeon, Woojun Kim, Whiyoung Jung, and Youngchul Sung. 2022. Maser: Multi-agent reinforcement learning with subgoals generated from experience replay buffer. In International Conference on Machine Learning. PMLR, 10041– 10052. [9] Afshin OroojlooyJadid and Davood Hajinezhad. 2019. A review of cooperative multi-agent deep reinforcement learning. arXiv preprint arXiv:1908.03963 (2019) [10] Tabish Rashid, Mikayel Samvelyan, Christian Schroeder De Witt, Gregory Farquhar, Jakob Foerster, and Shimon Whiteson. 2018. QMIX: monotonic value function factorisation for deep multi-agent reinforcement learning. arXiv preprint arXiv:1803.11485 (2018). [11] Ryan Lowe, Yi Wu, Aviv Tamar, Jean Harb, OpenAI Pieter Abbeel, and Igor Mordatch. 2017. multi-agent actor-critic for mixed cooperative-competitive environments. In Advances in Neural Information Processing Systems. 6379–6390. [12] Jakob N Foerster, Gregory Farquhar, Triantafyllos Afouras, Nantas Nardelli, and Shimon Whiteson. 2018. Counterfactual multi-agent policy gradients. In Thirty-second AAAI conference on artificial intelligence. [13] Christian Schroeder de Witt, Jakob Foerster, Gregory Farquhar, Philip Torr, Wendelin Böhmer, and Shimon Whiteson. 2019. Multi-Agent Common Knowledge Reinforcement. [14] Ying Wen, Yaodong Yang, Rui Luo, Jun Wang, and Wei Pan. 2019. Probabilistic recursive reasoning for multi-agent reinforcement learning. arXiv preprint arXiv:1901.09207 (2019). [15] Natasha Jaques, Angeliki Lazaridou, Edward Hughes, Caglar Gulcehre, Pedro A Ortega, DJ Strouse, Joel Z Leibo, and Nando De Freitas. 2018. Social influence as intrinsic motivation for multi-agent deep reinforcement learning. arXiv preprint arXiv:1810.08647 (2018). [16] T. M. Cover and J. A. Thomas. 2006. Elements of Information Theory. Wiley. [17] Tonghan Wang, Jianhao Wang, Yi Wu, and Chongjie Zhang. 2019. Influence-based multi-agent exploration. arXiv preprint arXiv:1910.05512 (2019). [18] Shakir Mohamed and Danilo J Rezende. 2015. Variational information maximisation for intrinsically motivated reinforcement learning. In Proceedings of the 28th International Conference on Neural Information Processing Systems-Volume 2. 2125–2133. [19] Minghuan Liu, Ming Zhou, Weinan Zhang, Yuzheng Zhuang, Jun Wang, Wulong Liu, and Yong Yu. 2020. Multi-Agent Interactions Modeling with Correlated Policies. arXiv preprint arXiv:2001.03415 (2020). [20] Ying Wen, Yaodong Yang, Rui Luo, Jun Wang, and Wei Pan. 2019. Probabilistic recursive reasoning for multi-agent reinforcement learning. arXiv preprint arXiv:1901.09207 (2019). [21] Foerster, J. N., et al. (2016). Learning to communicate with deep multi-agent reinforcement learning. In Advances in Neural Information Processing Systems. [22] Sunehag, P., et al. (2018). Value-Decomposition Networks for Cooperative Multi-Agent Learning. In International Conference on Machine Learning. [23] Babu, A. S., et al. (2020). A Variational Approach to Mutual Information-Based Coordination for Multi-Agent Reinforcement Learning. arXiv preprint arXiv:2012.12527. [24] Zhao, T., et al. (2019). Hybrid Reinforcement Learning with Information-Driven Models for Sparse State Spaces. In International Conference on Machine Learning.

Copyright

Copyright © 2024 Priyanka S Chauhan, Ajay Prakash Nair , Vadlamudi Neel Vittal Bharath , Pragati Narote . This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.